Implicit Solvation Models#

One aproach to include solvent effects on your calculation is through the so-called "implicit solvent models", and here we will discuss two main options available in ORCA.

Overview#

In these models, the solute is placed in a cavity of roughly molecular shape. The solvent is described by a continuum that interacts with the charges on the cavity surface, which are in turn determined by the solute and the problem is solved iteratively (see [Cammi2005] for a good review on the subject).

The general picture of the method can be depicted as:

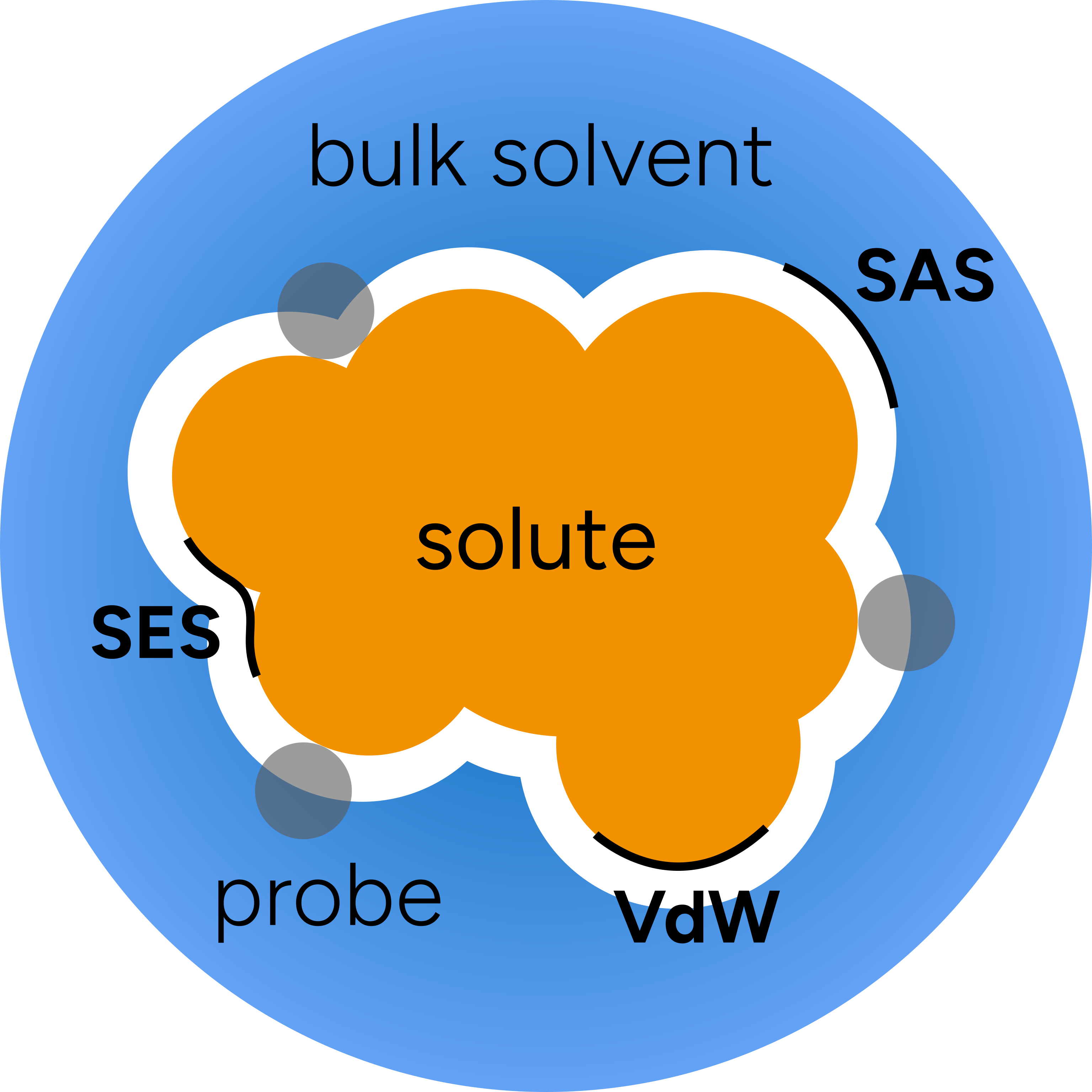
where the "probe" is an ideal solvent molecule and the molecular cavities are defined from:

"Van der Waals surface" (vdW), built from the Van der Waals radii (the default in ORCA);

"Solvent-Accessible Surface" (SAS), defined by the center of the probe;

or the "Solvent-Excluded Surface" (SES), obtained if you follow the inward part of the solvent probe sphere rolling over vdW surface.

The solvation energy is then decomposed in two main terms, electrostatic (\(\Delta G_{ENP}\)) and cavity-dispersion (\(\Delta G_{CDS}\)):

\[ \Delta G_{solv}^o = \Delta G_{ENP} + \Delta G_{CDS} \]

and the methods differ on how to compute these terms.

Transition from Gas to Liquid phase#

Depending on the desired reference state of your molecule, an additional term to the solvation free energy has to be included:

\[ \Delta G_{solv}^o = \Delta G_{ENP} + \Delta G_{CDS} + \Delta G^o_{conc} \]

This term arises when going from gas phase at \(1 atm\) and \(298 K\) (which is how the \(G^o\) is calculated when using FREQ by default) to a solution phase at \(1 molL^{-1}\). The corresponding correction [Cramer2004] is:

\[ \Delta G^o_{conc}= RTln(24.5) = 1.89 kcalmol^{-1}. \]

Warning

Do not forget to add this term to your \(G^o\) when predicting solution thermodynamics. The absence of this correction can lead to large errors!

Conductor-like Polarizable Continuum Model (CPCM)#

In the CPCM method [Cossi1998], the bulk solvent is treated as a conductor-like polarizable continuum and the main parameters to define the method are the refractive index and the dielectric constant of the medium.

The electrostatic contribution (\(\Delta G_{ENP}\)) that arises from the interaction of the medium and the molecular surface charges is included in the SCF calculation - so that you even get "solvated" orbitals - and the cavity term (\(\Delta G_{CDS}\)) can be obtained from more complicated schemes.

ORCA has a list of predefined solvents that can be called by using:

!CPCM(solvent)

where solvent can be any from:

Solvent Name	Dielec. Const.	Refrac. Index
Water	80.4	1.33
Acetone	20.7	1.359
Acetonitrile	36.6	1.344
Ammonia	22.4	1.33
Benzene	2.28	1.501
CCl4	2.24	1.466
CH2Cl2	9.08	1.424
Chloroform	4.9	1.45
Cyclohexane	2.02	1.425
DMF	38.3	1.430
DMSO	47.2	1.479
Ethanol	24.3	1.361
Hexane	1.89	1.375
Methanol	32.63	1.329
Octanol	10.3	1.421
Pyridine	12.5	1.510
THF	7.25	1.407
Toluene	2.4	1.497

If you want to include any other solvent, one can always input these parameters manually using:

%CPCM       EPSILON      80.4
            REFRAC       1.33
END

More options and details can be found on the ORCA manual. One example for the single-point calculation of an Aspirin molecule in water is:

!BP86 DEF2-SVP CPCM(WATER)
* XYZFILE 0 1 aspirin.xyz

Note

Both the analytic gradients and Hessians are available for the CPCM, so that can be used together with the OPT and FREQ keywords as well!

Then, before the SCF, a header with all the CPCM-related information is printed:

--------------------
CPCM SOLVATION MODEL
--------------------
CPCM parameters:
  Epsilon                                         ...      80.4000
  Refrac                                          ...       1.3300
  Rsolv                                           ...       1.3000
  Surface type                                    ... GAUSSIAN VDW
  Epsilon function type                           ...         CPCM
Radii:
 Radius for C  used is    3.8550 Bohr (=   2.0400 Ang.)
 Radius for O  used is    3.4469 Bohr (=   1.8240 Ang.)
 Radius for H  used is    2.4944 Bohr (=   1.3200 Ang.)
Calculating surface                               ...        done! (  0.0s)
GEPOL surface points                              ...         1160
GEPOL Volume                                      ...    1403.2346
GEPOL Surface-area                                ...     757.5566
Calculating surface distance matrix               ...        done! (  0.0s)
Performing Cholesky decomposition & store         ...        done! (  0.1s)
Overall time for CPCM initialization              ...                 0.2s

after the SCF calculation ends, there will be a the summary of the CPCM-related information:

Components:
Nuclear Repulsion  :          765.01084602 Eh           20817.00344 eV
Electronic Energy  :        -1413.26452682 Eh          -38456.88288 eV
One Electron Energy:        -2400.58284083 Eh          -65323.18007 eV
Two Electron Energy:          987.31831400 Eh           26866.29718 eV
CPCM Dielectric    :           -0.01874113 Eh              -0.50997 eV
[...]
CPCM Solvation Model Properties:
Surface-charge          :           -0.01502552
Charge-correction       :           -0.00002872 Eh              -0.00078 eV
Free-energy (cav+disp)  :  This term is not implemented in the current solvation scheme

As one can see, dielectric contribution to the energy, the solute net charge, the charge and cavity corrections are printed separately (the latter in this case is not calculated). The Charge-correction term is not included in the SCF energy, and is just printed for information purposes.

The FINAL SINGLE POINT ENERGY now already includes all computed solvation terms. In terms of the equations shown above, \(\Delta G_{ENP}\) corresponds to CPCM Dielectric and \(\Delta G_{CDS}\) to the Free-energy (cav+disp).

Important

There is an important difference with respect to previous ORCA versions. Now the cavity term is not calculated or added for regular CPCM by default.

Note

For more information on cavity terms and CPCM, please consult the ORCA manual.

Combining DFT with post-HF methods#

Since the HF density is of lower quality than those obtained from DFT, so is the CPCM correction obtained from HF calculations.

What one usually can do is to take the \(\Delta G_{ENP}\) (CPCM Dielectric) and \(\Delta G_{CDS}\) (Free-energy (cav+disp)) from some calculation like DFT and add that to the total energy obtained with that method, e.g. if you want to combine CPCM with DLPNO-CSSD.

Gaussian point charges#

The usual point charge scheme might lead to instabilities in the energy, e.g. if two points end up too close. In ORCA, we use a smeared Gaussian charge to obtain a smoother potential energy surface [Karplus1999] [Neese2020] instead. From ORCA 5, the default is:

%CPCM SURFACETYPE VDW_GAUSSIAN END

But a SES surface can also be chosen with:

%CPCM SURFACETYPE GEPOL_SES_GAUSSIAN END

For more detailed information, please consult the ORCA manual

Universal Solvation Model (SMD)#

The SMD method [Truhlar2009] can be thought as an improvement over the CPCM, since it uses the full solute electron density to compute the cavity-dispersion contribution instead of the area only.

This method requires more parameters, which makes it less flexible for unknown solvents, but ORCA has currently 179 solvents available (ORCA manual)! In order to use it, add:

%CPCM SMD TRUE
      SMDSOLVENT "SOLVENT"
END

to the input. The same example from before would be:

!BP86 DEF2-SVP
%CPCM SMD TRUE
      SMDSOLVENT "WATER"
END
* XYZFILE 0 1 aspirin.xyz

The initial output is similar to CPCM, except that one now has the SMD descriptors:

SMD-CDS solvent descriptors:
  Soln                                       ...    1.3328
  Soln25                                     ...    1.3323
  Sola                                       ...    0.0000
  Solb                                       ...    0.0000
  Solg                                       ...    0.0000
  Solc                                       ...    0.0000
  Solh                                       ...    0.0000

and the output before the the TOTAL SCF ENERGY header has:

CPCM Dielectric    :           -0.02952804 Eh              -0.80350 eV
SMD CDS (Gcds)     :            0.01088483 Eh               0.29619 eV

One can use this \(\Delta G_{CDS}\) (Gcds) term, together with the \(\Delta G_{ENP}\) (CPCM Dielectric) to correct energies from further calculations.

Dynamic Radii Adjustment for COntinuum solvation (DRACO)#

All these solvation models depend on a physically sound representation of the solvent accessible surface area (SASA). Nevertheless, the typically employed methods use a predefined set of element specific atomic radii to construct it. This does not account for the molecular environment of specific atoms for which the effective radii may differ depending on the respective local electron density, e.g., if one compares neutral and negatively charged oxygen atoms. A recent approach to make these radii environment adaptive is the DRACO model by Grimme and co-workers [Grimme2024]. It uses an atoms-in-molecules-like approach based on atomic partial charges and fractional coordination numbers to scale the default radii for each atom independently. By doing so, specifically the description of charged systems can be improved.

DRACO is currently available for CPCM and SMD within ORCA and is parameterized for the solvents water, acetonitrile, DMSO, and methanol. DRACO can be envoked by a simple input keyword in addition to the respective solvation method:

! CPCM(solvent) DRACO

! SMD(solvent) DRACO

Alternatively, it can also be requested in the %cpcm block:

%cpcm
DRACO true
end

In ORCA, the default scheme to calculate the partial charges used within DRACO is the electronegativity-equilibration (EEQ) charge model as it is also used in the D4 dispersion correction. However, one can also request the recent Charge Extended Hückel (CEH) model.[Grimme2023] The charge scheme within DRACO is controlled by the following tag in the %cpcm block:

%cpcm
draco_charges ceh  # default = eeq
end

If CEH charges are requested, ORCA generates them via its interface to the xtb program.

Note

At this point, DRACO can only be used in single-point energy calculations. Gradients for DRACO will be implemented in the future.

Example: Octanol/Water Partition Coefficient#

We will use SMD and try to predict the octanol/water partition coefficient (\(P_{o/w}\)) for the drug Diazepam:

\[ P_{o/w} = \frac {[solute]_{octanol}} {[solute]_{water}} \]

That can be obtained from the relationship between the equilibrium constant and the Gibb's free energy difference between the solute in octanol and water \(\Delta G^o_{o/w} = \Delta G^o_{o} - \Delta G^o_{w}\) as [Truhlar2009]:

\[ logP_{o/w} = \frac {-\Delta G^o_{o/w}} {2.303RT} \]

First, we optimize both geometries in each solvent, for instance using:

!B3LYP DEF2-SVP OPT NUMFREQ D4
%CPCM SMD TRUE
      SMDSOLVENT "1-OCTANOL"
END
* XYZFILE 0 1 diazepam.xyz

or:

!B3LYP DEF2-SVP OPT NUMFREQ D4
%CPCM SMD TRUE
      SMDSOLVENT "WATER"
END
* XYZFILE 0 1 diazepam.xyz

to get the Gibbs free energy of each solvated compound and its geometry. Here is an image of the molecule with a VdW cavity surface in blue:

After making the calculations, one obtains an energy difference of \(3.41 kcalmol^{-1}\), that corresponds to a \(logP_{o/w}=2.50\), which is not far from the experimental value of \(logP_{o/w}^{exp}=2.99\), considering the simplicity of the method.

Note

Since there are no analytic frequencies using the SMD model yet, we are using !NUMFREQ. It might take long if you do not parallelization here.

CPCM and COSMO#

ORCA does not have any COSMO implementation, but one can use the COSMO epsilon function by using the CPCMC(solvent) keyword, with an extra "C":

!B3LYP DEF2-SVP CPCMC(WATER)

Implicit Solvation Models#

Overview#

Transition from Gas to Liquid phase#

Conductor-like Polarizable Continuum Model (CPCM)#

Combining DFT with post-HF methods#

Gaussian point charges#

Universal Solvation Model (SMD)#

Dynamic Radii Adjustment for COntinuum solvation (DRACO)#

Example: Octanol/Water Partition Coefficient#

CPCM and COSMO#

Starting structures#