Thermodynamics#

If you have successfully done a Vibrational frequencies calculation, now you have access to the thermodynamic functions such as enthalpy (\(H\)), entropy (\(S\)) and the Gibbs free energy (\(G\))!

Let's follow an example and use this to predict the relative enthalpy ordering of some butadiene isomers.

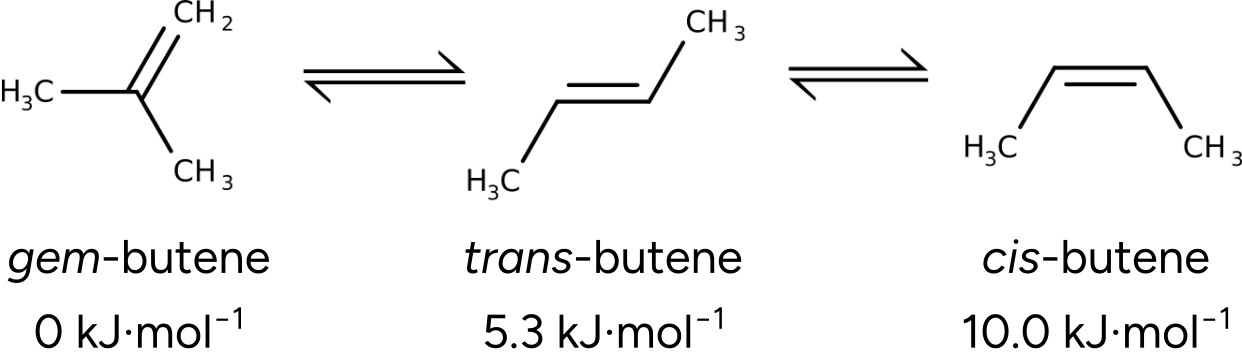
../_images/butene.png — Figure: Experimental relative free energies of *gem*-, *trans*-, and *cis*-butene (T = 298.15 K, p = 1 atm).#

using the following keywords and the geminal isomer as an example:

!B3LYP D4 DEF2-TZVP OPT FREQ
* XYZFILE 0 1 gem-butene.xyz

Thermodynamic functions#

Assuming you had !FREQ on the input, immediately after the frequencies and normal modes, one will see that the thermochemistry section starts:

Temperature         ...   298.15 K
Pressure            ...     1.00 atm  
Total Mass          ...    56.11 AMU
Quasi RRHO          ...     True
Cut-Off Frequency   ...     1.00 cm^-1 

Note

These properties will be computed for a given temperature and pressure, assuming a gas-phase molecule and using statistical mechanics. For thermodynamics in solution, check the Implicit Solvation Models section.

Inner energy#

The first function is the inner energy (\(U\)), that is computed following the output:

------------
INNER ENERGY
------------

The inner energy is: U= E(el) + E(ZPE) + E(vib) + E(rot) + E(trans)
    E(el)   - is the total energy from the electronic structure calculation
              = E(kin-el) + E(nuc-el) + E(el-el) + E(nuc-nuc)
    E(ZPE)  - the the zero temperature vibrational energy from the frequency calculation
    E(vib)  - the the finite temperature correction to E(ZPE) due to population
              of excited vibrational states
    E(rot)  - is the rotational thermal energy
    E(trans)- is the translational thermal energy

Summary of contributions to the inner energy U:
Electronic energy                ...   -157.18614555 Eh
Zero point energy                ...      0.10746477 Eh      67.44 kcal/mol
Thermal vibrational correction   ...      0.00246995 Eh       1.55 kcal/mol
Thermal rotational correction    ...      0.00141627 Eh       0.89 kcal/mol
Thermal translational correction ...      0.00141627 Eh       0.89 kcal/mol
-----------------------------------------------------------------------
Total thermal energy                   -157.07337829 Eh

The Electronic energy is what you get from the FINAL SINGLE POINT ENERGY, then the Zero-Point Energy (ZPE) is calculated, together with the Thermal correction, which has to do with the rotational, vibrational and translational degrees of freedom.

The Total correction is amount the of energy you have to add to your FINAL SINGLE POINT electronic energy to convert \(E_{el}\) into \(U\).

Enthalpy#

Then the calculation of the enthalpy. That is simply \(U + k_BT\):

--------
ENTHALPY
--------

The enthalpy is H = U + kB*T
                kB is Boltzmann's constant
Total thermal energy              ...   -157.07337829 Eh
Thermal Enthalpy correction       ...      0.00094421 Eh       0.59 kcal/mol
-----------------------------------------------------------------------
Total Enthalpy                    ...   -157.07243408 Eh

Again, the Thermal Enthalpy correction is what one has to add to \(U\) to compute \(H\).

Entropy#

The entropy term follows:

-------
ENTROPY
-------

The entropy contributions are T*S = T*(S(el)+S(vib)+S(rot)+S(trans))
     S(el)   - electronic entropy
     S(vib)  - vibrational entropy
     S(rot)  - rotational entropy
     S(trans)- translational entropy
The entropies will be listed as multiplied by the temperature to get
units of energy

Electronic entropy                ...      0.00000000 Eh      0.00 kcal/mol
Vibrational entropy               ...      0.00393432 Eh      2.47 kcal/mol
Rotational entropy                ...      0.01154964 Eh      7.25 kcal/mol
Translational entropy             ...      0.01805279 Eh     11.33 kcal/mol
-----------------------------------------------------------------------
Final entropy term                ...      0.03353675 Eh     21.04 kcal/mol

with its different components and a Final entropy term that is already multiplied by the temperature, the \(TS\) term that is latter used for the free energy.

Gibbs free energy#

Finally, the free energy term is printed:

-------------------
GIBBS FREE ENERGY
-------------------

The Gibbs free energy is G = H - T*S

Total enthalpy                    ...   -157.07243408 Eh
Total entropy correction          ...     -0.03353675 Eh    -21.04 kcal/mol
-----------------------------------------------------------------------
Final Gibbs free energy         ...   -157.10597083 Eh

For completeness - the Gibbs free energy minus the electronic energy
G-E(el)                           ...      0.08017472 Eh     50.31 kcal/mol

The last term, G-E(el) is the term that you would have to add to your electronic energy to transform \(E_{el}\) into \(G^o\) at a given temperature and pressure.

Note

This G-E(el) only depends on the geometry and frequencies, and thus can be computed in a lower level method, such as DFT, and later combined with the \(E_{el}\) of a higher level method, such as DLPNO-CCSD(T) to achieve a very good prediction of the \(G^o\)!

Comparison to experiment#

The Final Gibbs free energy values yield relative free energies of \(3.4\) \(kJ mol^{-1}\) and \(7.1\) \(kJ mol^{-1}\).

To improve the agreement with the experimental data, the electronic energy component \(E_{el}\) can also be computed at the DLPNO-CCSD(T) level. The respective values are given by the FINAL SINGLE POINT ENERGY.

!DLPNO-CCSD(T) aug-cc-pVTZ AUTOAUX RIJCOSX
* XYZFILE 0 1 butene_optimized_dft.xyz

These electronic energies are now corrected by the G-E(el) values from the DFT calculations.

Comparison of calculated versus experimental Gribbs free energies for butene isomers in kJ/mol#
Compound	\(\Delta E_{DFT} + \Delta G_{DFT}\)	\(\Delta E_{CCSD(T)} + \Delta G_{DFT}\)	\(\Delta G_{Exp.}\)
gem-butene	0.0	0.0	0.0
trans-butene	3.4	4.8	6.2
cis-butene	7.1	8.6	7.8

Thermodynamics at different temperatures#

To compute these thermodynamic properties at different temperatures, or at several, one can use:

%FREQ TEMP 77, 298, 330, 450 END

and the thermodynamic functions will be separated by the headers:

--------------------------
THERMOCHEMISTRY AT 77K
--------------------------
[...]
--------------------------
THERMOCHEMISTRY AT 298K
--------------------------
[...]

and so on.

Changing the temperature after the calculation#

If you want to compute thermodynamic functions after you calculation has already finished, that can be done setting a simple input such as:

!PRINTTHERMOCHEM
%GEOM
         INHESSNAME "basename.hess"
END
%FREQ TEMP 290, 295, 300
END
* XYZFILE 0 1 geometry.xyz

as one can save a lot of time from recalculations.

Note

One could use this to also include isotopic effects, by changing the masses in the basename.hess file and recomputing the thermodynamics (see Kinectic Isotope Effects (KIE)).

Thermodynamics#

Thermodynamic functions#

Inner energy#

Enthalpy#

Entropy#

Gibbs free energy#

Comparison to experiment#

Thermodynamics at different temperatures#

Changing the temperature after the calculation#

Structures#