Infrared and Raman#

The prediction of infrared (IR) and (non-resnonant) Raman spectra are nowadays a straightforward task in computational chemistry. Let us use ORCA to predict the fundamental frequencies and intensities for benzene.

../_images/benzene.png — Figure: D_6h symmetric structure of benzene.#

Because of its symmetry, the selection rules predict that these bands are mutually exclusive, with \(A_{2u}\) and \(E_{1u}\) modes being the most IR active (\(B_{1u}, B_{2u}\) and \(E_{2u}\) modes are less intense), while the \(A_{1g}, E_{1g}\) and \(E_{2g}\) are Raman active. For comparison, the complete set of experimental values can be found on NIST's website.

Predicting infrared spectra#

The optimization of the molecular structure and subsequent calculation of the vibrational frequencies, e.g. with DFT can be envoked via simple keywords OPT and FREQ:

!BP86 DEF2-SVP OPT FREQ

*XYZFILE 0 1 structure.xyz

For Grimme's efficient r²SCAN-3c composite DFT method the respective input is:

!r2SCAN-3c OPT FREQ

If no analytical Hessian is available for the chosen method, the NUMFREQ keyword can be used to request a numerical Hessian calculation.

After the successful calculation, the vibrational frequencies will be printed:

-----------------------
VIBRATIONAL FREQUENCIES
-----------------------

Scaling factor for frequencies =  1.000000000  (already applied!)

     0:       0.00 cm**-1
     1:       0.00 cm**-1
     2:       0.00 cm**-1
     3:       0.00 cm**-1
     4:       0.00 cm**-1
     5:       0.00 cm**-1
     6:     405.17 cm**-1
     7:     405.28 cm**-1
     8:     626.34 cm**-1
     9:     626.55 cm**-1
[...]

followed by the vibrational modes and the IR spectrum.

-----------
IR SPECTRUM
-----------

 Mode   freq       eps      Int      T**2         TX        TY        TZ
       cm**-1   L/(mol*cm) km/mol    a.u.
----------------------------------------------------------------------------
  6:    405.17   0.000000    0.00  0.000000  ( 0.000000  0.000000 -0.000000)
  7:    405.28   0.000000    0.00  0.000000  ( 0.000000 -0.000000  0.000109)
  8:    626.34   0.000000    0.00  0.000000  ( 0.000000  0.000000  0.000000)
  9:    626.55   0.000000    0.00  0.000000  (-0.000000  0.000000 -0.000000)
 10:    676.63   0.025862  130.70  0.011928  (-0.000000  0.000000 -0.109214)
[...]

where the dipole derivatives necessary to compute the IR intensities are printed after each frequency.

Plotting the IR spectrum#

The IR spectrum can then be immediately generated with any suitable GUI like Avogadro 2. Just open the saved output file basename.out and click on Analysis → Plot Spectra... to open a new window were the IR spectrum will be plotted:

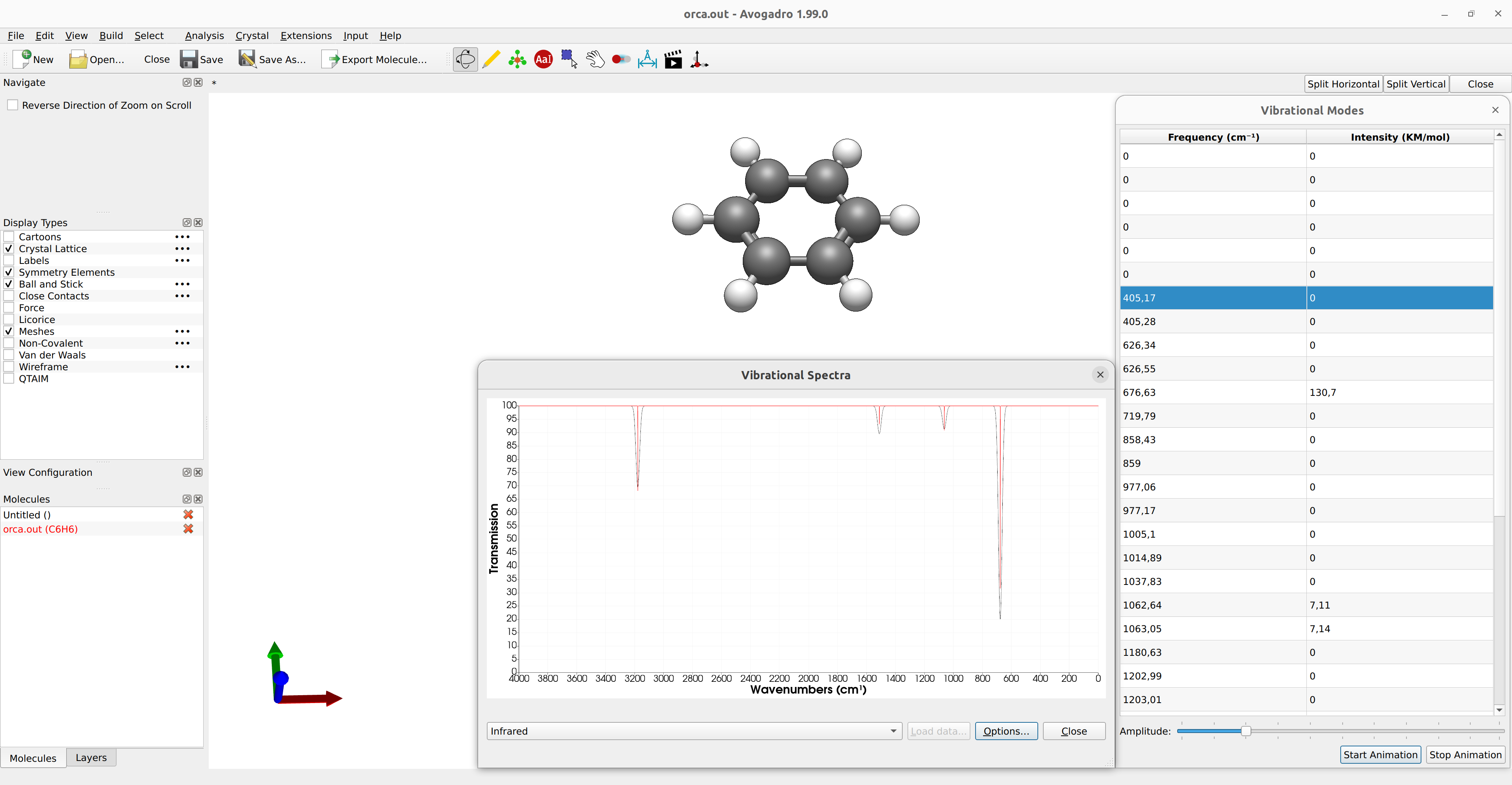
../_images/irspectrum-avogadro2.png — Figure: IR spectrum plotted with Avogadro 2.#

Visualizing modes#

In order to have a better assignment of the IR peaks, one can click on the corresponding frequency in the main Avogadro window and then on Start Animation to make a small movie of the mode displacement.

As an example, if one chooses the \(A_{2u}\) IR active mode at \(668 cm^{-1}\), that in textbooks is commonly assigned as an out-of-plane C-H bending, one gets:

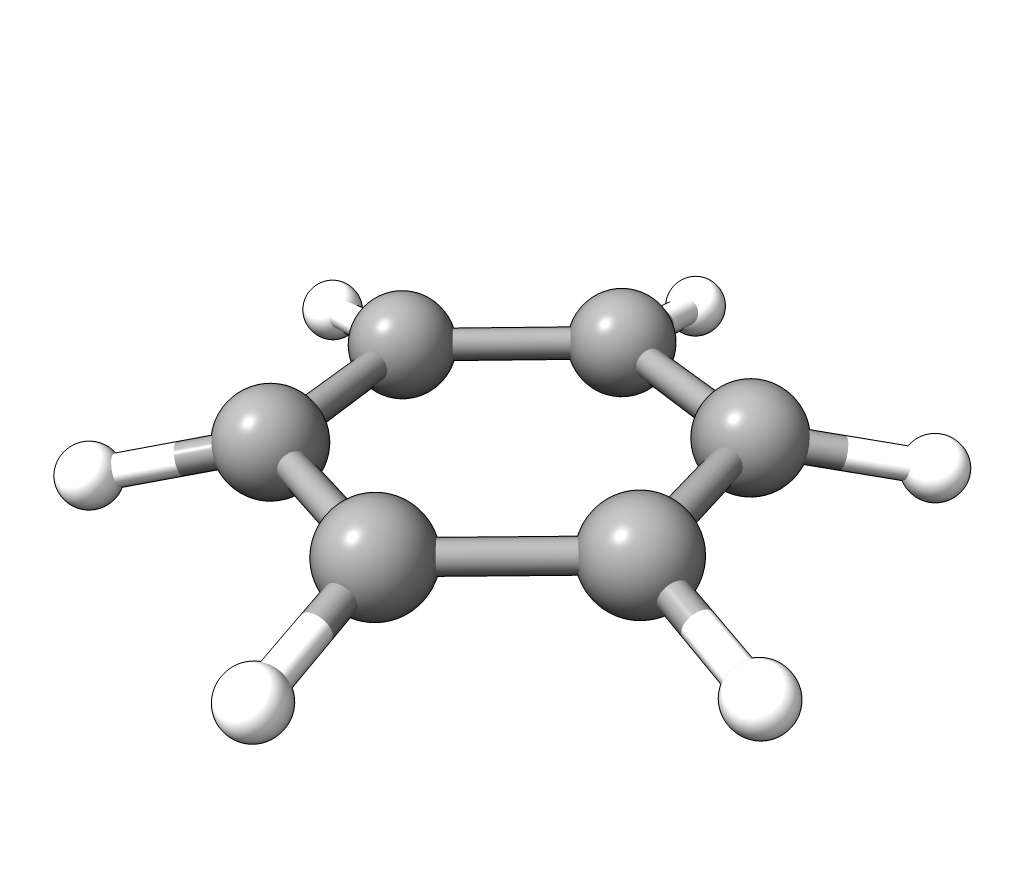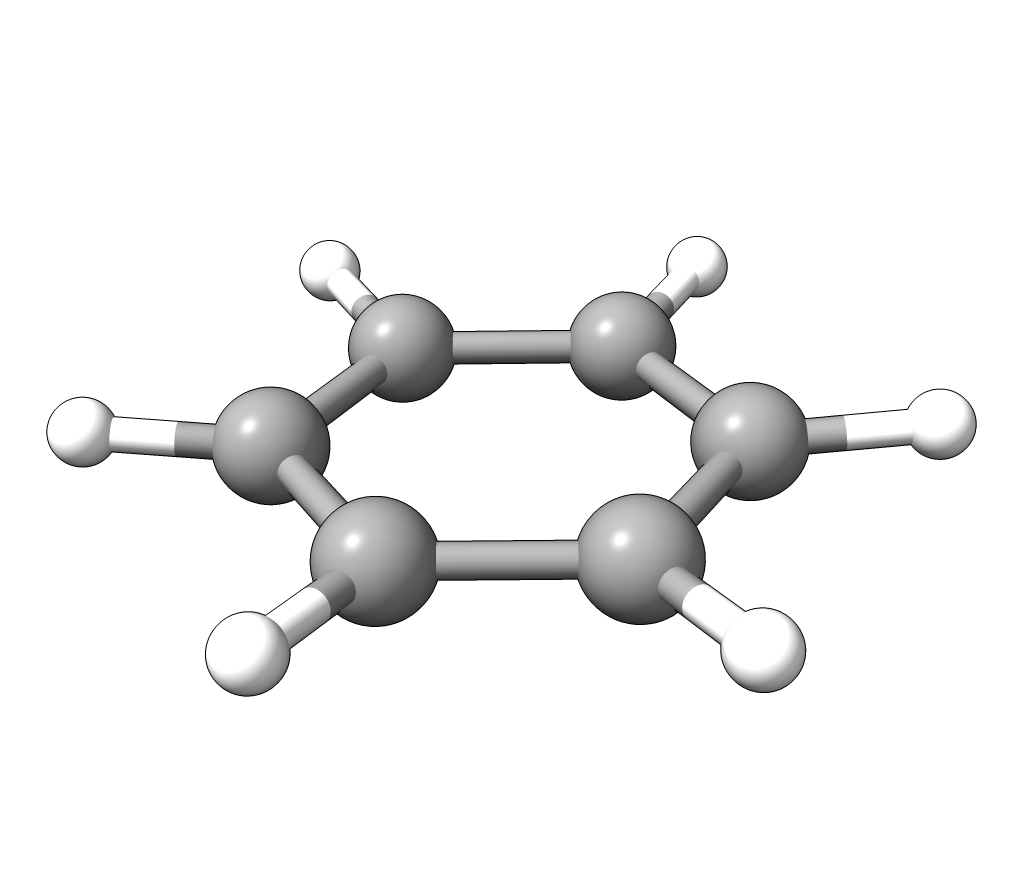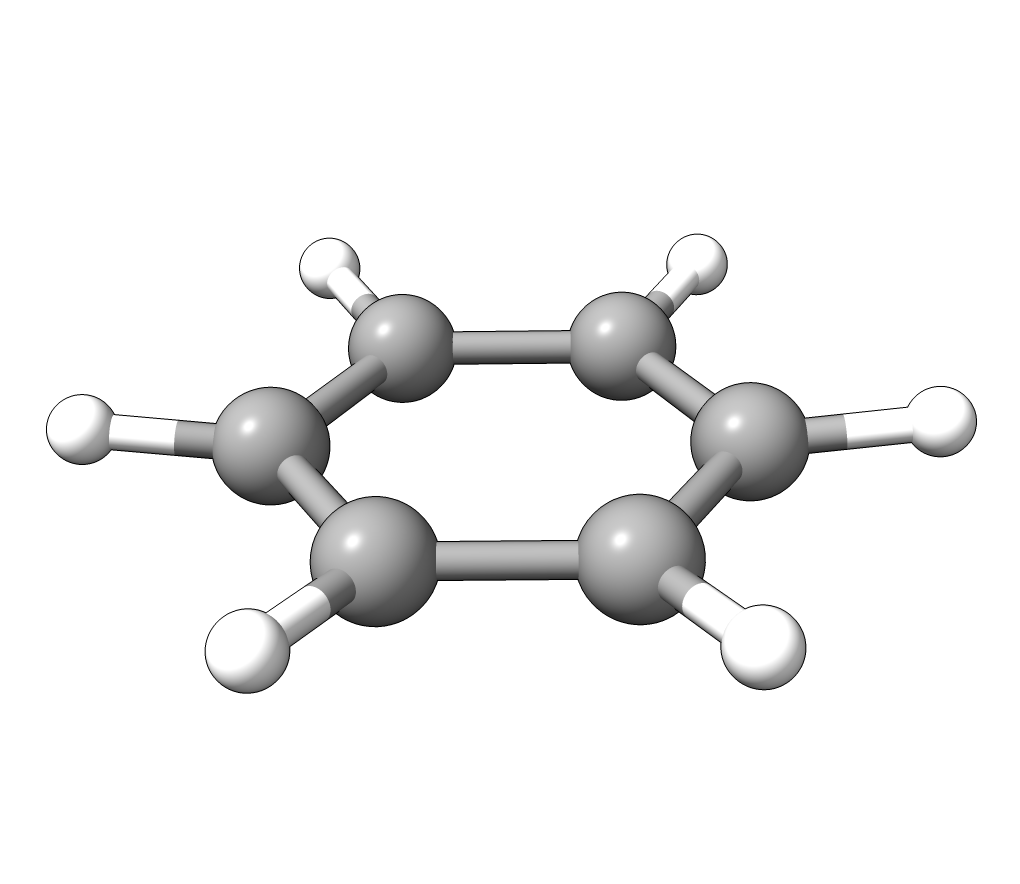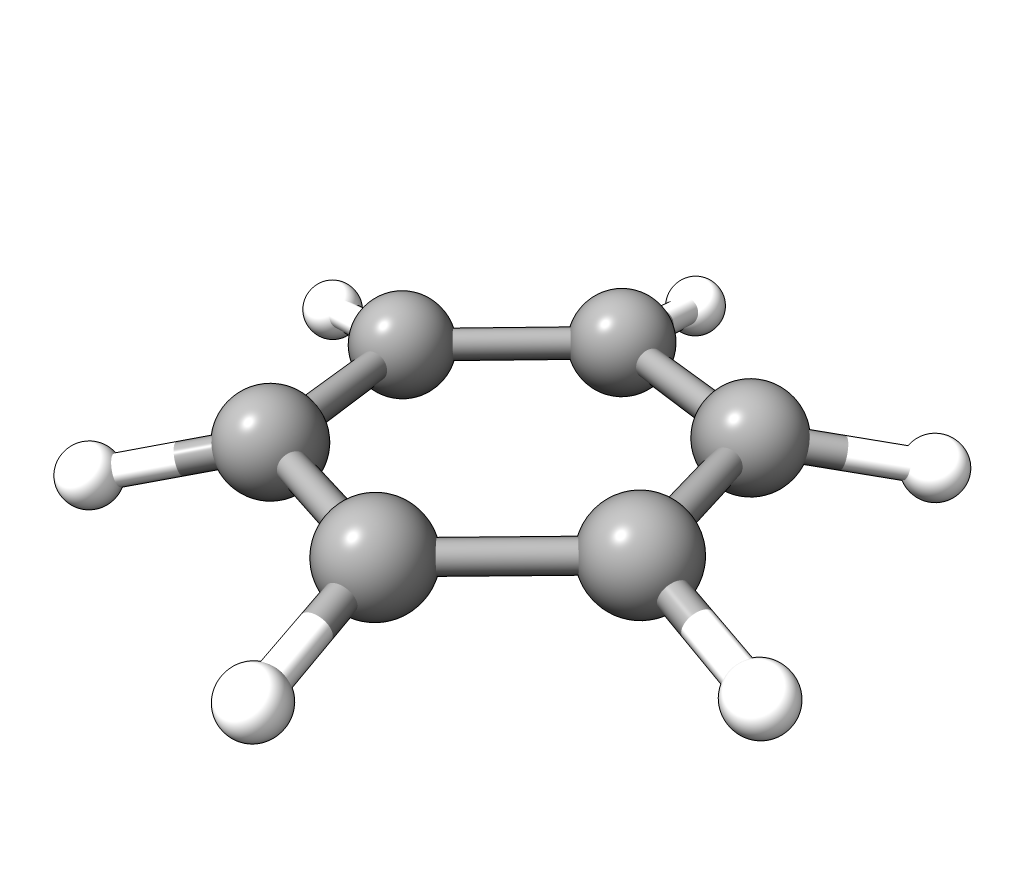
../_images/benzene.gif — Animation: \(A_{2u}\) IR active mode of benzene.#

exactly as expected. The symmetry breaking creates a temporary dipole one the benzene molecule, and that allows for intensity on a IR transition.

Note

The line broadening must be included ad hoc here because it is related to the lifetimes of vibrational excited states and structural parameters that were not accounted for in the calculation and might vary depending on the experimental conditions.

Important

Be aware that we are predicting only fundamental transitions, so no overtones and combination bands are included!

Here is a table comparing the calculated and experimental values for the IR fundamentals:

Comparison between predicted IR fundamental modes for benzene using r²SCAN-3c and the corresponding experimental values, in wavenumbers.#
Mode	Experiment / cm^-1	Predicted / cm^-1
\(E_{2u}\) Ring deform	410	405
\(A_{2u}\) C-H bend	673	676
\(B_{1u}\) Ring deform	1010	1005
\(E_{1u}\) C-H bend	1038	1037
\(B_{2u}\) C-H bend	1150	1180
\(E_{1u}\) C=C str	1486	1511
\(B_{1u}\) C-H str	3068	3179
\(E_{1u}\) C-H str	3063	3116

Predicting Raman spectra#

In a similar way, the non-resonant Raman spectra composed of fundamental transitions can be predicted. The main difference here is that the derivatives of the polarizability have to be computed numerically, so that the !NUMFREQ flag has to be used, together with a keyword under %ELPROP to request the calculation of polarizabilties:

!r2SCAN-3c OPT NUMFREQ

%ELPROP
   POLAR 1
END

*XYZFILE 0 1 structure.xyz

Note

Analytical Hessians are not available for Raman spectra calculations. Therefore, NUMFREQ must be used.

Here POLAR 1 means that the polarizability is computed analytically, by solving the CP-SCF equations. However, this option is only available for regular DFT and HF. For other methods, POLAR 2 can be chosen to compute it directly from the derivatives of the dipole moment. Please check the ORCA manual for all available options.

After successful termination the Raman spectrum is printed after the IR section and the Raman spectrum can be plotted with Avogadro analogous to the IR spectrum.

--------------
RAMAN SPECTRUM
--------------

 Mode    freq (cm**-1)   Activity   Depolarization
-------------------------------------------------------------------
   6:       406.22      0.000000      0.066146     
   7:       406.38      0.000001      0.035663    
   8:       620.29      6.321364      0.748913
   9:       626.43      6.122879      0.750000
  10:       677.12      0.000007      0.078694 
  11:       720.92      0.002478      0.749995 
  12:       859.04      3.481939      0.749999
[...]

It is important to say the Raman intensities are a more complicated subject than those of IR and are much more dependent on the experimental setup, that is why we print here the so-called "Raman Activity" instead [Hess2002], because it is setup invariant.

Again, we can compile a table comparing the calculated and experimental values for the Raman fundamentals:

Comparison between predicted Raman fundamental modes for benzene using r²SCAN-3c and the corresponding experimental values, in wavenumbers.#
Mode	Experiment / cm^-1	Predicted / cm^-1
\(E_{2g}\) Ring deform	606	620
\(E_{1g}\) C-H bend	849	859
\(A_{1g}\) Ring str	992	977
\(E_{2g}\) C-H bend	1178	1197
\(A_{2g}\) C-H bend	1326	1374
\(E_{2g}\) Ring str	1606/1585	1630
\(E_{2g}\) C-H str	3047	3177
\(A_{1g}\) C-H str	3062	3186

Scaling frequencies#

Please also note the Scaling factor for frequencies printed in the output just before the frequency values. These are empirical factors that can be used to multiply all frequencies and correct for errors from theory [Martin2014]. It can be controlled by setting the SCALFREQ flag under %FREQ. For example, the previous reference suggest a scaling factor of 0.9956 for BP86/DEF2-SVP.

!BP86 DEF2-SVP FREQ
%FREQ
   SCALFREQ 0.9956
END
* XYZFILE 0 1 structure.xyz

Note

If one is using Avogadro, these scaling factor can be added later by setting the "Scale Factor" on the "Infrared Spectra Settings" tab shown before.

Warning

Negative frequencies mean that your system is not in real minimum! Please check the Removing negative frequencies section for more info on that.

Infrared and Raman#

Predicting infrared spectra#

Plotting the IR spectrum#

Visualizing modes#

Predicting Raman spectra#

Scaling frequencies#

Starting structures#