Kinectic Isotope Effects (KIE)#

Kinetic isotope effects (KIE) are changes in reaction rates caused by a change in a given isotope in a molecule. That is caused due to the difference in mass, that affects vibrational frequencies and/or tunneling probabilities.

It is an effect often exploited to investigate reaction mechanisms, when there is bond breaking or forming to an atom that can be substituted by an isotope. These KIE are predictable, depending on the mass ratios, and thus can be used to validate proposed mechanisms. The origin of the KIE is related to a change on the Zero Point Energy (ZPE) of the system, that is affected when the vibrational frequencies are lowered or increased due to the mass change. For the heavier deuterium the vibrational frequencies are lowered, thus lowering the ZPE and altering the free energy barrier.

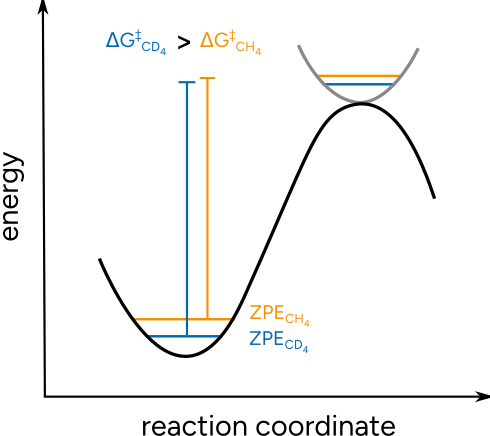
../_images/kie.png — Figure: Schematic origin of the KIE.#

Typically, the KIE is quantified by the ratio of the reaction rates of both reactions \(\frac {k_H} {k_D}\). This can be calculated from the free energy reaction barriers of both reactions according to:

\[ \frac {k_H} {k_D} = e^{-(\Delta G^{\ddagger}_H - \Delta G^{\ddagger}_D) / RT} \]

To obtain these barriers, we can use the usual transition state search and optimization algorithms in ORCA, we just have to adjust the mass of the respective atoms to simulate the corresponding isotopes. This can be easily done via the geometry input within the ORCA input file:

!wB97X-3c

* XYZ 0 1
  H     -2.411352    1.128722    0.029849		<= Hydrogen
  H     -1.342943    1.352019   -0.097229 M 2.00141	<= Deuterium
*

Here, we adjusted the mass of H to 2.00141 amu which corresponds to deuterium.

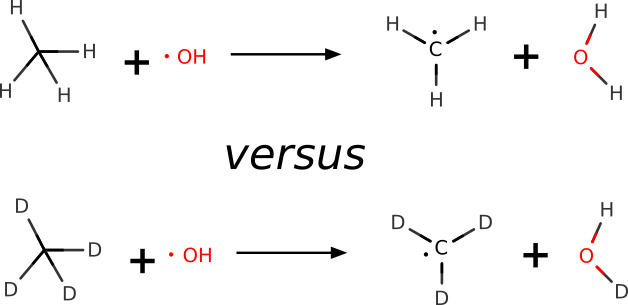
Example 1: H-atom Abstraction#

In this example, we use ORCA to make a quantum-mechanical prediction of the KIE for the H-atom abstraction from methane by the hydroxyl radical. The respective KIE ratio is known from highly accurate gas-phase experiments (\(6.75 \pm 0.83\)).[Tully1993]

First, we searched for the transition states of the respective reactions with the NEB-TS method. In this case, we employed the ωB97X-3c composite method. It is based on a range-separated hybrid functional that is specifically suited to compute transition states and reaction barriers at a reasonable cost. Note, that we also adjusted the temperature for the thermochemistry calculation to obtain free energies at the same conditions as in the experiment (T = 293 K). We further optimize the isolated reactants for both cases. The respective inputs can be found in the tabs below:

NEB-TS CH₄

!wB97X-3c NEB-TS FREQ

%FREQ   
 TEMP 293     
END

%NEB 
 NEB_END_XYZFILE "products.xyz"
 PREOPT_ENDS true
END

*XYZ 0 2
C     -2.42007     1.14475     0.00503
H     -1.37176     1.42602    -0.24888
H     -2.95035     0.87504    -0.97240
H     -2.97696     2.02414     0.50780
H     -2.39461     0.26127     0.72431
O      1.11295     1.79481    -0.12688
H      0.85814     0.90892     0.95813
*

NEB-TS CD₄

!wB97X-3c NEB-TS FREQ

%FREQ   
 TEMP 293     
END

%NEB 
 NEB_END_XYZFILE "products-deuterated.xyz"
 PREOPT_ENDS true
END

*XYZ 0 2
C     -2.42007     1.14475     0.00503
H     -1.37176     1.42602    -0.24888 M 2.00141
H     -2.95035     0.87504    -0.97240 M 2.00141
H     -2.97696     2.02414     0.50780 M 2.00141
H     -2.39461     0.26127     0.72431 M 2.00141
O      1.11295     1.79481    -0.12688
H      0.85814     0.90892     0.95813
*

Opt OH

!wB97X-3c OPT FREQ

%FREQ   
 TEMP 293 
END

*XYZ 0 2
O      1.11295     1.79481    -0.12688
H      0.85814     0.90892     0.95813
*

Opt CH₄

!wB97X-3c OPT FREQ

%FREQ   
 TEMP 293 
END

* XYZ 0 1
C     -2.42007     1.14475     0.00503
H     -1.37176     1.42602    -0.24888
H     -2.95035     0.87504    -0.97240
H     -2.97696     2.02414     0.50780
H     -2.39461     0.26127     0.72431
*

Opt CD₄

!wB97X-3c OPT FREQ

%FREQ 
 TEMP 293 
END

* XYZ 0 1
C     -2.42007     1.14475     0.00503
H     -1.37176     1.42602    -0.24888 M 2.00141
H     -2.95035     0.87504    -0.97240 M 2.00141
H     -2.97696     2.02414     0.50780 M 2.00141
H     -2.39461     0.26127     0.72431 M 2.00141
*

After the successful NEB-TS calculations, we obtain the respective optimized transition states:

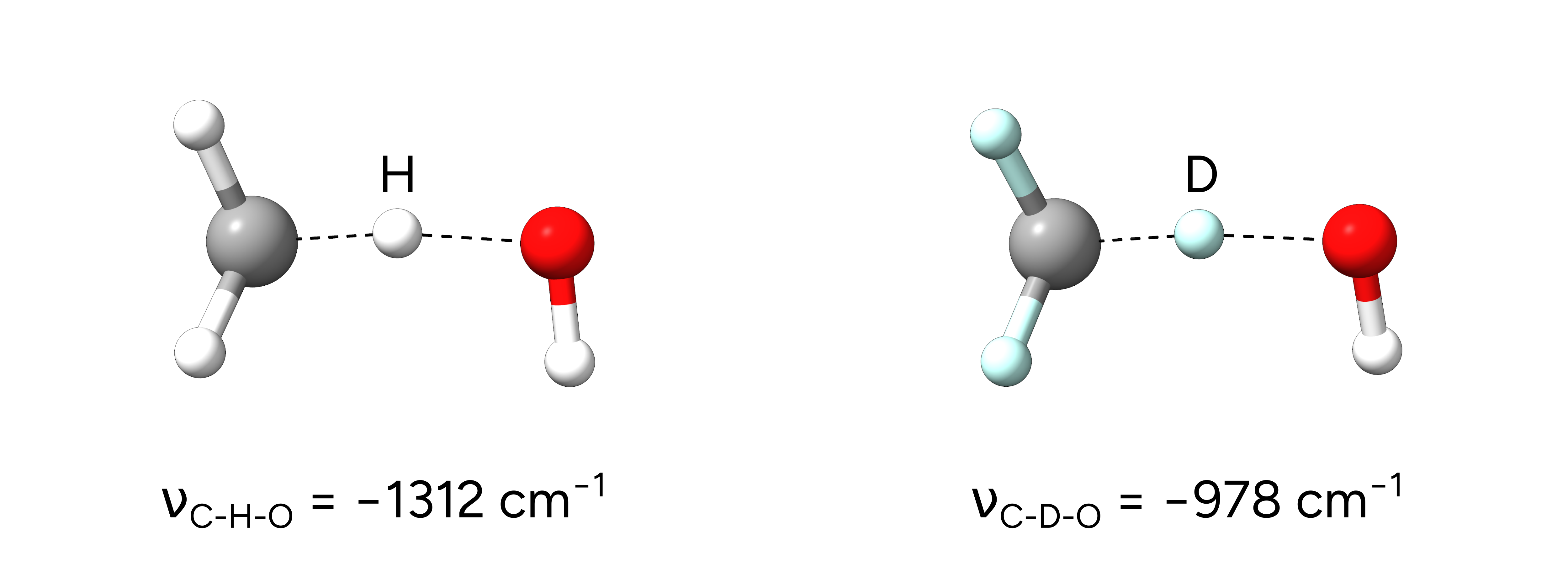
../_images/kie-ts.png — Figure: Transition states of the H-atom abstraction from methane and deuterated methane.#

Single imaginary frequencies of -1312.67 \(cm^{-1}\) for the hydrogen case and -978.70 \(cm^{-1}\) for the deuterated transition state verify the structures to be true transition states and already reflect the KIE.

The activation barriers \(\Delta G_H^{\ddagger}\) are now calculated as the difference of the free energy of the transition state and the sum of the free energies of the isolated reactants. For our example, we obtain 47.63 and 53.51 \(kJ \cdot mol^{-1}\), respectively. From these values, a \(\frac {k_H} {k_D}\) ration of 7.17 is calculated. This value is in excellent agreement with the experimental value of \(6.75 \pm 0.83\).

Important

By simply computing the KIE in terms of changes on the free energy barriers like that, we are not considering any tunneling effects. Those can be quite important, and sometimes need to be included using one of various different approaches, e.g. [Aquilanti2019].

Kinectic Isotope Effects (KIE)#

Example 1: H-atom Abstraction#

Structures#